Simple abstract
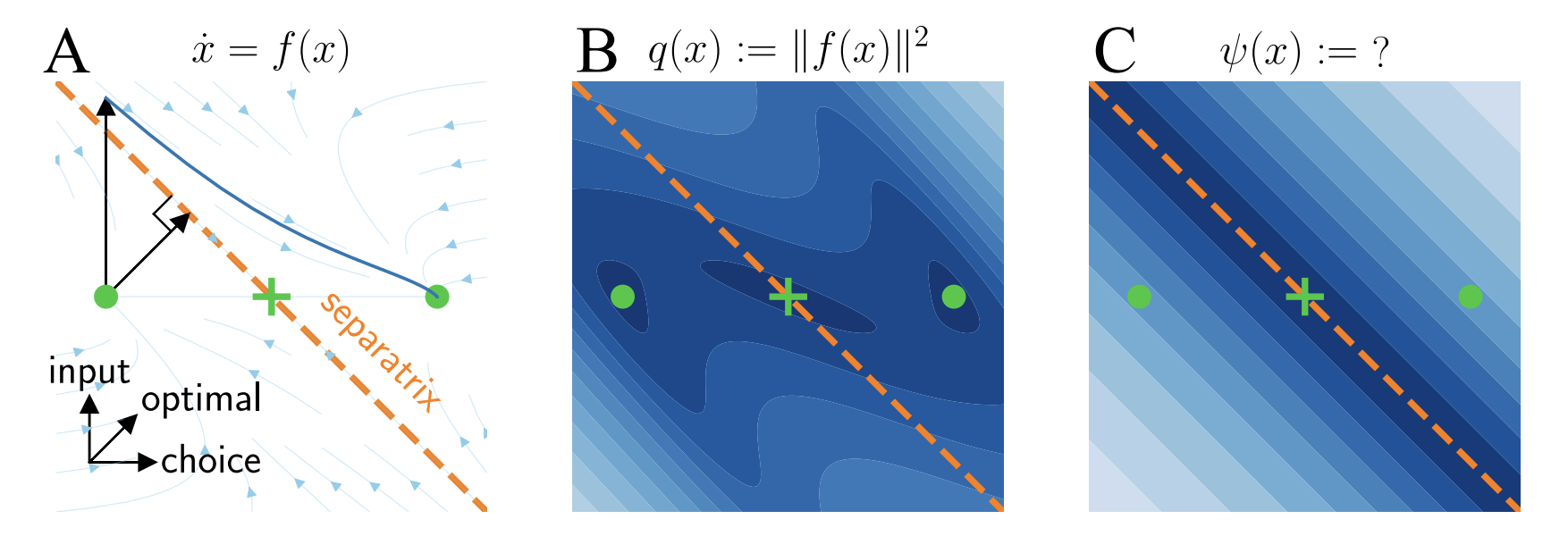
When you make a decision, your brain crosses a decision boundary. In the language of dynamical systems, this boundary is called a separatrix in the system’s phase space, because states on either side of it proceed to evolve very differently, ultimately converging to different attractors. We develop a numerical method based on Koopman theory to charaterise this boundary, provided the dynamical function, i.e., a complete description of the system dynamics. We demonstrate our method on several synthetic examples, trained RNNs and a model of microbiome ecology fit to experimental data. We demonstrate the method’s utility in designing optimal perturbations to push a system across its separatrix.
Citation
Dabholkar, Kabir V., and Omri Barak. “Finding separatrices of dynamical flows with Deep Koopman Eigenfunctions.” arXiv preprint arXiv:2505.15231 (2025).
@article{dabholkar2025finding,
title={Finding separatrices of dynamical flows with Deep Koopman Eigenfunctions},
author={Dabholkar, Kabir V and Barak, Omri},
journal={arXiv preprint arXiv:2505.15231},
year={2025}
}